Detecting and Eliminating Quantum Noise of Quantum Measurements

Abstract

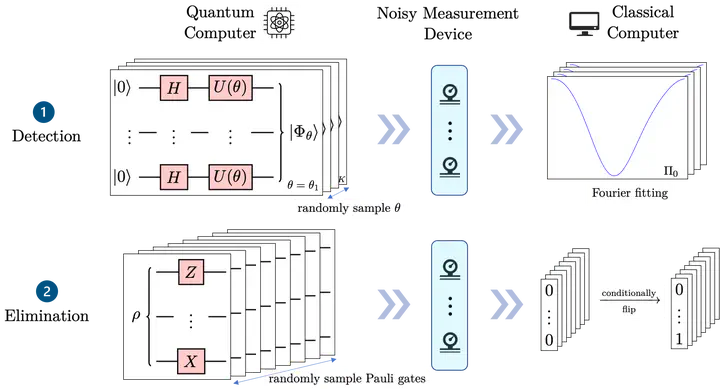
In this work, we propose a two-stage procedure to systematically address quantum noise inherent in quantum measurements. The idea behind it is intuitive: we first detect and then eliminate quantum noise so that the classical noise assumption is satisfied and measurement error mitigation works. In the first stage, inspired by coherence witness in the resource theory of quantum coherence, we design an efficient method to detect quantum noise. It works by fitting the difference between two measurement statistics to the Fourier series, where the statistics are obtained using maximally coherent states with relative phase and maximally mixed states as inputs. The fitting coefficients quantitatively benchmark quantum noise. In the second stage, we design various methods to eliminate quantum noise, inspired by the Pauli twirling technique. They work by executing randomly sampled Pauli gates before the measurement device and conditionally flipping the measurement outcomes in such a way that the effective measurement device contains only classical noise. We demonstrate the feasibility of the two-stage procedure numerically on Baidu Quantum Platform. Remarkably, the results show that quantum noise in measurement devices is significantly suppressed, and the quantum computation accuracy is substantially improved. We highlight that the two-stage procedure complements existing measurement error mitigation techniques, and they together form a standard toolbox for manipulating measurement errors in near-term quantum devices.