Dense Coding with Locality Restriction on Decoders: Quantum Encoders versus Superquantum Encoders
Abstract
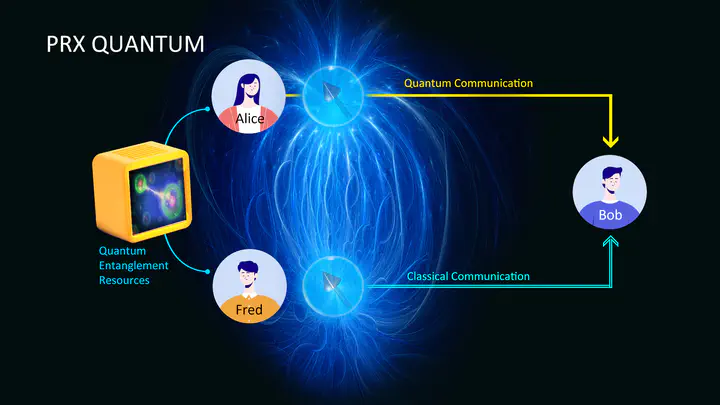
We investigate practical dense coding by imposing locality restrictions on decoders and symmetry restrictions on encoders within the resource theory of asymmetry framework. In this task, the sender Alice and the helper Fred preshare an entangled state. Alice encodes a classical message into the quantum state using a symmetric preserving encoder and sends the encoded state to Bob through a noiseless quantum channel. The receiver Bob and helper Fred are limited to performing quantum measurements satisfying certain locality restrictions to decode the classical message. We are interested in the ultimate dense coding capacity under these constraints. Our contributions are summarized as follows. First, we derive both one-shot and asymptotic optimal achievable transmission rates of the dense coding task under different encoder and decoder combinations. Surprisingly, our results reveal that the transmission rate cannot be improved even when the decoder is relaxed from one-way local operations and classical communication (LOCC) to two-way LOCC, separable measurements, and partial transpose positive measurements of the bipartite system. Second, depending on the class of allowed decoders with certain locality restrictions, we relax the class of encoding operations to superquantum encoders in the general probability theory framework and derive dense coding transmission rates under this setting. For example, when the decoder is fixed to a separable measurement, theoretically, a positive operation is allowed as an encoding operation. Remarkably, even under this superquantum relaxation, the transmission rate still cannot be lifted. This fact highlights the universal validity of our analysis on practical dense coding beyond quantum theory.
Brief Summary
Dense coding is one of the earliest and most prominent quantum protocols that reveal the power of quantum entanglement in communication. Although it has been intensively studied, it has typically been restricted to scenarios where the receiver can perform global measurements to decode information, which is experimentally challenging. Thus, it is natural to impose locality conditions on the decoders from a practical perspective.
In this work, we explore the practicality of dense coding by elaborating 21 classes of dense coding capacities with different encoder-decoder pairs, where the encoders are constrained by the resource theory of asymmetry and the decoders are constrained by various locality conditions. Our contributions are to 1) show that all these capacities are equal and derive a single-letter capacity formula; 2) prove that all these capacities satisfy the desirable strong converse property; and 3) establish an equivalence among three different quantities of a bipartite quantum state—the operationally defined dense coding capacity, the mathematically defined regularized asymmetry of assistance, and the quantum entropy of the twirled quantum state—thus providing the regularized asymmetry of the assistance measure an operational meaning.
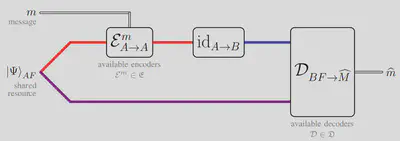
Our results significantly push forward the research of practical dense coding in both the one-shot and asymptotic regimes within different resource theories. These results deepen our understanding of quantum entanglement and dense coding, and, more generally, the classical and quantum communication via quantum resources.
Published in *PRX Quantum*.