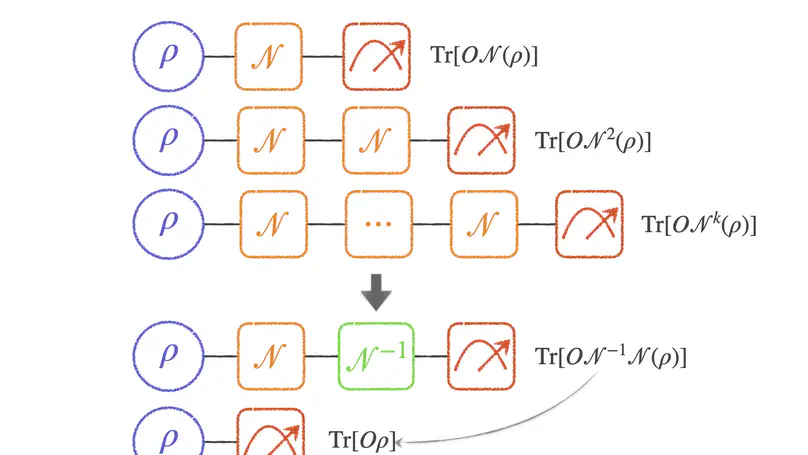
Quantum gates and measurements on quantum hardware are inevitably subject to hardware imperfections that lead to quantum errors. Mitigating such unavoidable errors is crucial to explore the power of quantum hardware better. In this paper, we propose a unified framework that can mitigate quantum gate and measurement errors in computing quantum expectation values utilizing the truncated Neumann series. The essential idea is to cancel the effect of quantum error by approximating its inverse via linearly combining quantum errors of different orders produced by sequential applications of the quantum devices with carefully chosen coefficients. Remarkably, the estimation error decays exponentially in the truncated order, and the incurred error mitigation overhead is independent of the system size, as long as the noise resistance of the quantum device is moderate. We numerically test this framework for different quantum errors and find that the computation accuracy is substantially improved. Our framework possesses several vital advantages: it mitigates quantum gate and measurement errors in a unified manner, it neither assumes any error structure nor requires the tomography procedure to completely characterize the quantum errors, and most importantly, it is scalable. These advantages empower our quantum error mitigation framework to be efficient and practical and extend the ability of near-term quantum devices to deliver quantum applications.

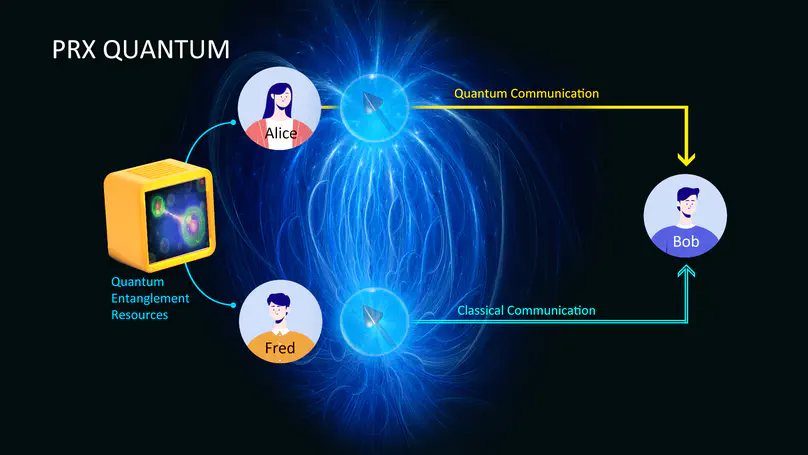
We investigate practical dense coding by imposing locality restrictions on decoders and symmetry restrictions on encoders within the resource theory of asymmetry framework. In this task, the sender Alice and the helper Fred preshare an entangled state. Alice encodes a classical message into the quantum state using a symmetric preserving encoder and sends the encoded state to Bob through a noiseless quantum channel. The receiver Bob and helper Fred are limited to performing quantum measurements satisfying certain locality restrictions to decode the classical message. We are interested in the ultimate dense coding capacity under these constraints. Our contributions are summarized as follows. First, we derive both one-shot and asymptotic optimal achievable transmission rates of the dense coding task under different encoder and decoder combinations. Surprisingly, our results reveal that the transmission rate cannot be improved even when the decoder is relaxed from one-way local operations and classical communication (LOCC) to two-way LOCC, separable measurements, and partial transpose positive measurements of the bipartite system. Second, depending on the class of allowed decoders with certain locality restrictions, we relax the class of encoding operations to superquantum encoders in the general probability theory framework and derive dense coding transmission rates under this setting. For example, when the decoder is fixed to a separable measurement, theoretically, a positive operation is allowed as an encoding operation. Remarkably, even under this superquantum relaxation, the transmission rate still cannot be lifted. This fact highlights the universal validity of our analysis on practical dense coding beyond quantum theory.

In a recent work [Pallister, Linden, and Montanaro, Phys. Rev. Lett. 120, 170502 (2018)], Pallister et al. proposed an optimal strategy to verify nonmaximally entangled two-qubit pure states under the constraint that the accessible measurements are locally projective and nonadaptive. Their good result leads naturally to the following question: What is the optimal strategy among general local operations and classical communication (LOCC) measurements? In this paper, we answer this problem completely for two-qubit pure states. To be specific, we give the optimal strategy for each of the following available classes of measurements: (i) local operations and one-way classical communication (one-way LOCC) measurements; (ii) local operations and two-way classical communication (two-way LOCC) measurements; and (iii) separable measurements. Surprisingly, our results reveal that for the two-qubit pure state verification problem two-way LOCC measurements remarkably outperform one-way LOCC measurements and have the same power as the separable measurements.

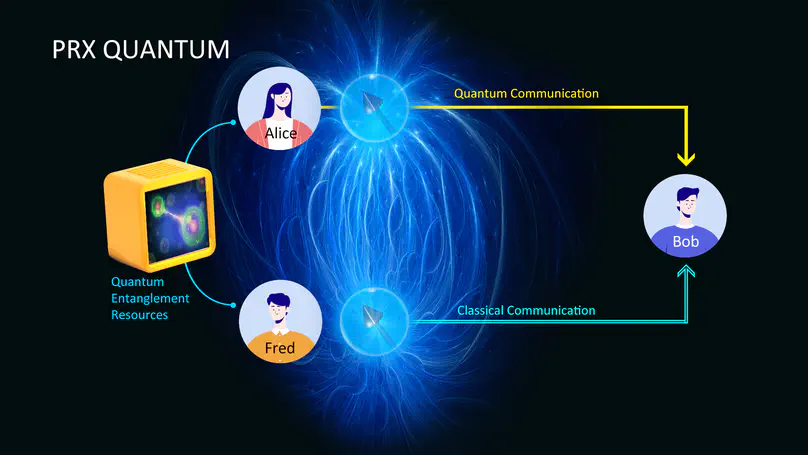
The researchers explored the practicality of dense coding by elaborating 21 classes of dense coding capacities with different encoder-decoder pairs, where the encoders are constrained by the resource theory of asymmetry and the decoders are constrained by various locality conditions.

As I read the wiki entry on Transfinite number, some problems come to my mind. Take Finite out of Infinite what is left after I take a finite subset out of an infinite set?

A Turing machine simulator that can simulates the turing machine described in the book “Introduction to Models of Computation”.

Recent research by a team at Southern University of Science and Technology (SUSTech) introduced a new resource theory of quantum channels and applied it to study communication over quantum channels.